Equivalence of algebraic structures
Consider two finite algebras that are the same except for a relabeling of the operations. Our intuition tells us that these are simply different names for the same mathematical structure. Formally, however, not only are these distinct mathematical objects, but also they are nonisomorphic.
Isotopy is another well known notion of “sameness” that is broader than isomorphism. However, I recently proved a result that shows why isotopy also fails to fully capture algebraic equivalence. $\def\bA{\bf A} \def\bB{\bf B} \def\bC{\bf C}$
This post provides a little bit of background and motivation, with a couple of examples of the problems that arise when trying to decide whether two algebraic objects are “equivalent.”
Example
Let us consider an example of two algebras that are the same except for the naming of their operations. (This is an elaboration on Exercises 5.1 in Algebras, Lattices, Varieties.)
Let $\bA$ be an algebra of size 4 and label the elements of the universe $\{1,2,3,4\}$. Suppose $\bA$ has two unary operations, $f^\bA$ and $g^\bA$, where $f^\bA$ is the permutation $(1,2)(3,4)$ and $g^\bA$ is the permutation $(1,3)(2,4)$.
Thus, the operations permute the elements as follows:
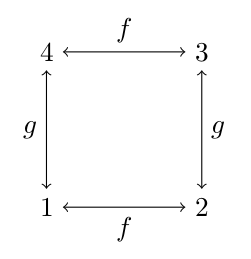
The congruence lattice of $\bA$ is
where, by abuse of notation, we identify the congruences with their corresponding partitions as follows:
Now consider the algebras $\mathbf{A}/\theta_1$, $\mathbf{A}/\theta_2$, and $\mathbf{A}/\theta_3$ which have respective universes
It is clear that
Also, no two factors are isomorphic. This is because of the naming of their respective operations.
The algebra $\mathbf{A}/\theta_1$ has operations $f^{\bA/\theta_1}$ and $g^{\bA/\theta_1}$, where $g^{\bA/\theta_1}$ permutes the blocks $\{1, 2\}\longleftrightarrow \{3, 4\}$ and $f^{\bA/\theta_1}$ leaves them fixed.
On the other hand, the algebra $\bA/\theta_2$ has operations $f^{\bA/\theta_2}$ and $g^{\bA/\theta_2}$, where $f^{\bA/\theta_2}$ permutes the blocks $\{1, 3\} \longleftrightarrow \{2, 4\}$ and $g^{\bA/\theta_2}$ leaves them fixed.
Thus, the operation in $\bA/\theta_1$ corresponding to the symbol $f$ is the identity, while in $\bA/\theta_2$ the $f$ symbol corresponds to the nonidentity permutation. But apart from this trivial relabeling, these two algebraic structures are the same.
This may be viewed as a minor technical issue that could be overcome by simply viewing the two algebras as nonindexed algebras (see, e.g., Polák), and we can certainly say that up to a relabeling of the operation symbols, the two algebras are isomorphic.
However, it would be preferable to have a notion of algebraic equivalence that did not hinge on operation alignment.
Deeper problems
The example above was a simple, almost trivial illustration of how the notion of isomorphic (indexed) algebras fails to capture our intuitive understanding of what it means for two algebras to be structurally the same. But there are examples that go deeper and are not as easy to side step.
Consider the Oates-Powell Theorem 1 which states that the variety generated by a finite group has a finite equational basis.
In a 1982 paper Roger Bryant proved that if we merely single out an element of the group and giving it a label, then the resulting algebra (called a pointed group) generates a variety that need not be finitely based.
Isotopy
Any reasonable notion of algebraic equivalence should at least respect congruences lattice structure. The congruence relations of algebras are the kernels of homomorphisms, and the congruence lattice is a basic “algebraic” feature of an algebra. Certainly we cannot accept a notion of “sameness” that equates two algebras with different congruence lattices (puting aside for now what it means for two congruence lattices to be “different”).
Isotopy provides a notion of “sameness” of algebras that is less demanding than isomorphism, so there is some hope that it provides a reasonably intuitive notion of algebraic equivalence.
But by the foregoing remark, if isotopy is to serve as a notion of algebraic equivalence, we should at least demand that two isotopic algebras have the “same” congruence lattices, and for two lattices to be the “same” in any sense, they must have the same number of elements so that we can at least find a bijection between them (even if it is not a “structure preserving” bijection).
However, I recently proved that, for any number $N \in \mathbb{N}$, it’s easy to construct a pair of isotopic algebras with congruence lattices that differ in size by more than $N$ elements. We see from this that there is no hope for isotopy as a reasonable notion of algebraic equivalence. (A link to my short article describing the construction appears below.)
Later, we will explore Voevodsky’s univalence principle and try to write down the definitions of universal algebras as higher types so that we can exploit the ideas of homotopy type theory in order to possibly arrive at a more useful, intuitionistic definition of algebraic equivalence.
Open GitHub repository
The Isotopy GitHub repository contains my article in which I present isotopic algebras with congruence lattices that are vastly different in size.
References
- [1] “Identical relations in finite groups,” S. Oates, M. B. Powell, J. Algebra (1965).
- [2] “The laws of finite pointed groups” R. M. Bryant, Bull. London Math. Soc, 14 (1982), 119-123.

