This post describes the steps I use to update or install multiple versions of the Java Development Kit (JDK) on Linux machines.
William DeMeo
about
I am a postdoc in the Math Department at University of Hawaii (2016–2017). In fall 2017 I will move to University of Colorado, Boulder.
I have worked at Iowa State University (2014–2016) and University of South Carolina (2012–2014).
My primary research area is universal algebra; current projects focus on lattice theory, computational complexity, and universal algebraic approaches to constraint satisfaction problems. Other research interests include logic, computability theory, type theory, category theory, functional programming, dependent types, and proof-carrying code.
Most of my research papers are posted on my Math arXiv page or my CS arXiv page. A more comprehensive collection of my work resides in my Github repositories.

Commutator as Least Fixed Point
The alt-comm repository contains a note giving an alternate decription of the (non-modular) commutator that yields a polynomial time algorithm for computing it. This is inspired by the alternate description of the commutator given by Kearnes in [1].
Conferences in Algebra
I started a GitHub repository called UniversalAlgebra/Conferences in an effort to keep up with the vast number of meetings in these areas and help make summer travel plans accordingly.
The UniversalAlgebra/Conferences repository is simply a list of links to the conferences listed.
Congruences of Partial Algebras
The repository par-alg-rep contains some notes describing a few results that we worked out in the fall of 2016, while I was a postdoc at University of Hawaii, although the main result—a straight-forward proof of the fact that every finite lattice is the congruence lattice of a finite partial algebra—was discovered during a visit to Chapman University in October 2016.
3-SAT and Partition Lattices
It is not hard to see that 3-SAT reduces to the problem of deciding whether all coatoms in a certain partition lattice are contained in the union of a collection of certain principal filters. Therefore, the latter problem, which we will call the covered coatoms problem (CCP), is NP-complete. In this post we simply define CCP. Later we check that 3-SAT reduces to CCP, and then develop some ideas about constructing a feasible algorithm to solve CCP.
Jane Street Test
The questions below appeared on an online test administered by Jane Street Capital Management to assess whether a person is worthy of a phone interview.
Learn You an Agda
This is a markdown version of the tutorial Learn You an Agda and Achieve Enlightenment! by Liam O’Connor-Davis.
I made this version for my own reference, while working through the tutorial, making some revisions and additions, and a few corrections. You may prefer the original.
Isotopy
Equivalence of algebraic structures
Consider two finite algebras that are the same except for a relabeling of the operations. Our intuition tells us that these are simply different names for the same mathematical structure. Formally, however, not only are these distinct mathematical objects, but also they are nonisomorphic.
Isotopy is another well known notion of “sameness” that is broader than isomorphism. However, I recently proved a result that shows why isotopy also fails to fully capture algebraic equivalence.
A Problem of Pálfy and Saxl
Suppose the lattice shown below is a congruence lattice of an algebra.
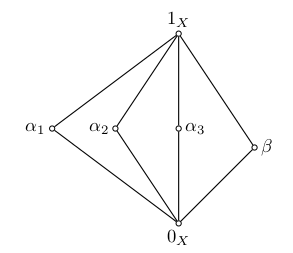
Claim: If the three $\alpha_i$’s pairwise permute, then all pairs in the lattice permute.
TypeFunc
I started a GitHub repository called TypeFunc in an effort to get my head around the massive amount of online resources for learning about type theory, functional programming, category theory, $\lambda$-calculus, and connections between topology and computing.

